CANCELED, will be presented next semester
Date: 7 November 2012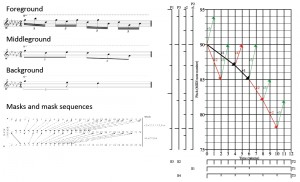
Time: 13.00-14.00
Place: NJ14 3-228 (Las Vegas)
The work described here takes its starting point in the idea that the best ways of understanding a particular musical object are those that are represented by the shortest possible descriptions of that object. I also propose that the goals of both music analysis and music perception are to find the shortest possible descriptions of musical objects. Note that a musical “object” could be a short musical fragment, a song, a multi-movement work or even a whole corpus of pieces. The goal of the research presented in this talk is to design an encoding language capable of expressing parsimonious descriptions of musical objects. This language must be able to express the types of equivalence relations that occur between musical structures, since a description of an object can often be shortened (i.e., compressed) by taking advantage of such equivalences that exist between parts of the object. The most important type of equivalence in music is translational equivalence within pitch-time space. However, musical translation is different from Euclidean geometric translation because pitch-time space can be transformed by pitch alphabets (periodic subsets of the pitch dimension) and rhythms (periodic subsets of the time dimension). Common examples of pitch alphabets are the usual scales and chords used in tonal music. Both pitch alphabets and rhythms can be represented by periodic masks, organised into mask sequences. Examples will be given of parsimonious descriptions (encodings) of musical objects that employ masks and mask sequences and an algorithm will be introduced that attempts to find such encodings from in extenso descriptions of musical objects.